欢迎进入某某教育官方网站!
咨询热线:400-123-4567
机器学习必知必会:凸优化
发布时间:2024-04-22 15:04:33
凸优化问题(OPT,convex optimization problem)指定义在凸集中的凸函数最优化的问题。尽管凸优化的条件比较苛刻,但仍然在机器学习领域有十分广泛的应用。
是凸集,如果对于任意的
和任意的
满足
时,
恒成立
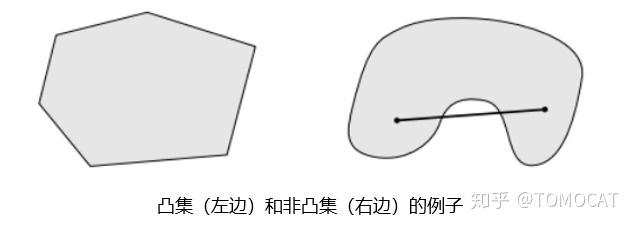
直观来说,任取一个集合中的两点练成一条线段,如果这条线段完全落在该集合中,那么这个集合就是凸集。
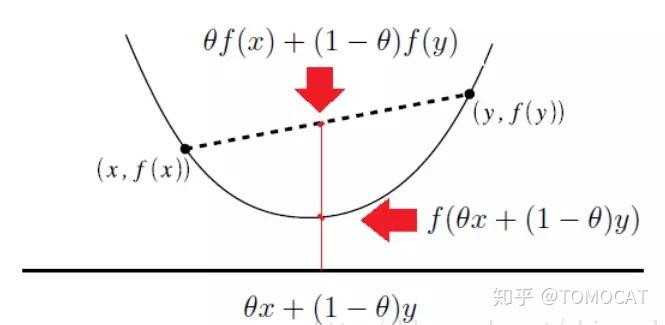
定义在 上的函数
是凸函数,如果它的定义域
是一个凸集且对任意的
和
,
恒成立
假设定义在 上的函数
ff可微(即对于所有 ,梯度
均存在)。则函数
是凸函数当且仅当函数定义域
是一个凸集,且对于所有
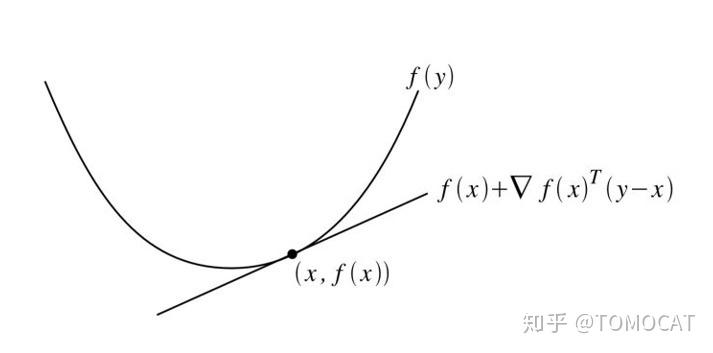
均满足:
一阶充要条件从几何意义上讲,即定义域内所有函数值都大于等于该点的一阶近似。
记函数的一阶导数和二阶导数分别为 和
:
假设定义在 上的函数
二阶可微(即对于所有
,海森矩阵
均存在)。则函数
是凸函数当且仅当函数定义域
是一个凸集,且对于所有
均满足:
注意:这里的表示的是半正定。
正定矩阵的概念是从正定二次型引入的,对称矩阵为正定的充要条件即该矩阵的特征值全为正数。
为方便理解正定/半正定矩阵,我们引入二次型 ,对于含有
个变量的二次齐次函数,我们可以一般化地写为:
同时,对于所有的二次齐次式我们都可以写成矩阵形式:
如果对任意的 均有
,则称
为正定二次型,同时称
为正定矩阵。
因为对于任意的二次型,我们都能将其写为矩阵形式,且矩阵的形式为:

因此二次型矩阵和对称矩阵是一一对应的关系。
对于最简单的一元二次函数 ,当
时
恒成立。即一元正定二次型对应的图像是开口向上,顶点在原点的抛物线,同理二元正定二次型
对应的图像是开口向上,顶点在原点的抛物面。
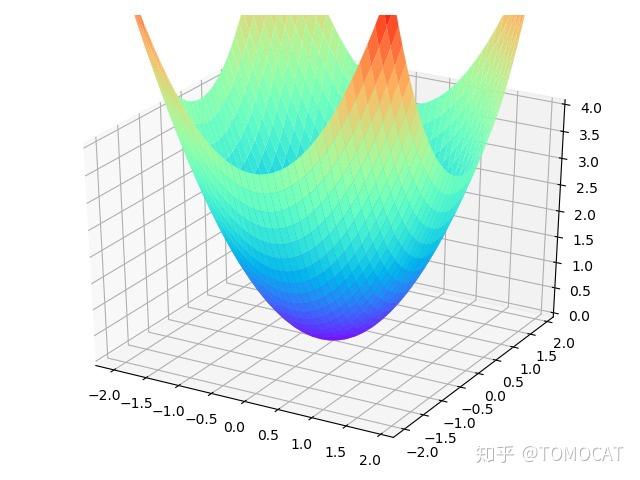
扩展到 元正定二次型的图像也对应着一个抛物线,保证当自变量取值非零向量时,对应的函数值大于0恒成立。
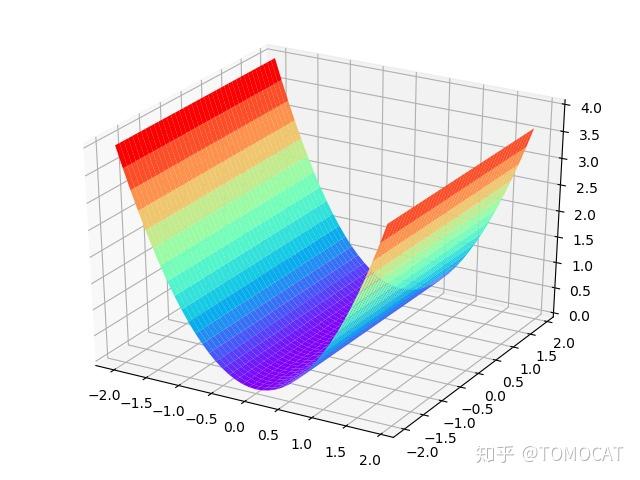
同样我们可以给出二元半正定二次型的图像,即某个自变量的特征值为 从而保证当自变量取值为非零向量时,对应的函数值大于等于
恒成立。
当 和
均为凸函数,而
均为仿射函数时, 上述的优化问题即凸优化问题。
?
其中目标函数和不等式约束都是仿射函数,且 表示按元素小于等于。
其中目标函数为凸二次型,不等式约束为仿射函数。
其中目标函数和不等式约束都是凸二次型。
其中需要最优化的变量 是一个对称的半正定矩阵,且
?为对阵矩阵。
由于凸优化问题具有局部最优解即全局最优解的优良特性,因此求解过程可以简化为:找到一个点列使得目标函数值持续减少,直到触发停止条件或达到一个最小值。
设
?为第 次迭代的值,
?为第 次搜索方向,
为第
次迭代的步长,则第
次迭代公式为:
其中第 次的搜索方向满足:
[1]https://www.jiqizhixin.com/articles/2019-03-05-8
[2]https://www.zhihu.com/question/38902714/answer/195435181
[3]https://www.jianshu.com/p/62539b0316e2
[4]plot: matplotlib.pyplot
[5]http://cs229.stanford.edu/section/cs229-cvxopt.pdf